Simple DSA Question That Hurt My Ego : But Valuable Lessons Learned

Question

Problem Statement

Input and Output Formats

Time and Space constrains

Sample Test Cases

Input

4
4
<<>>
4
>><<
5
>>>>>
7
<><><><

Output

Algorithm I came up with

Idea

We just have to simulate a stack ;

One idea is to start from 0, whenever we see >, we push to the stack, when we see <, we pop from the stack.

A better phrasing would be to change a variable initially set to 0, according to the same rules - add 1 if you see '<' otherwise subtract 1.

I had learnt a trick recently in C++ :-

c += (ch=='<') 1 ? : -1 ;

In one line, we can capture the entire algorithm.

Answer

So total number of distinct elements would be :-

The maximum up the stack can go + The minimum level to which stack can go + 1

Or :-

max(c) + | min(c) | + 1

Visualization of this Algorithm

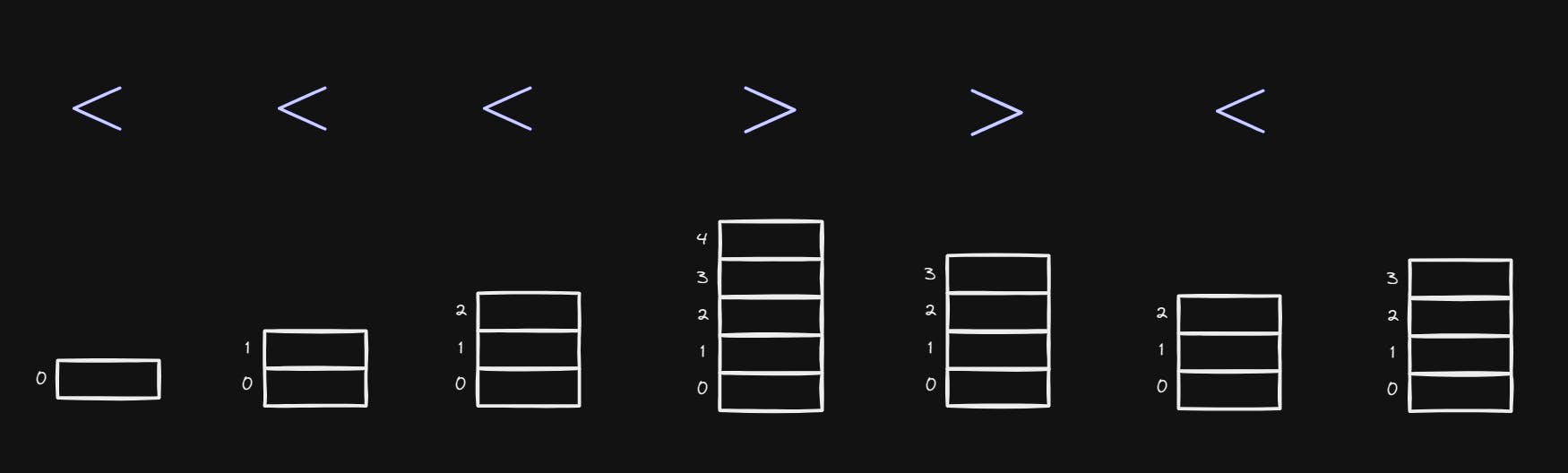
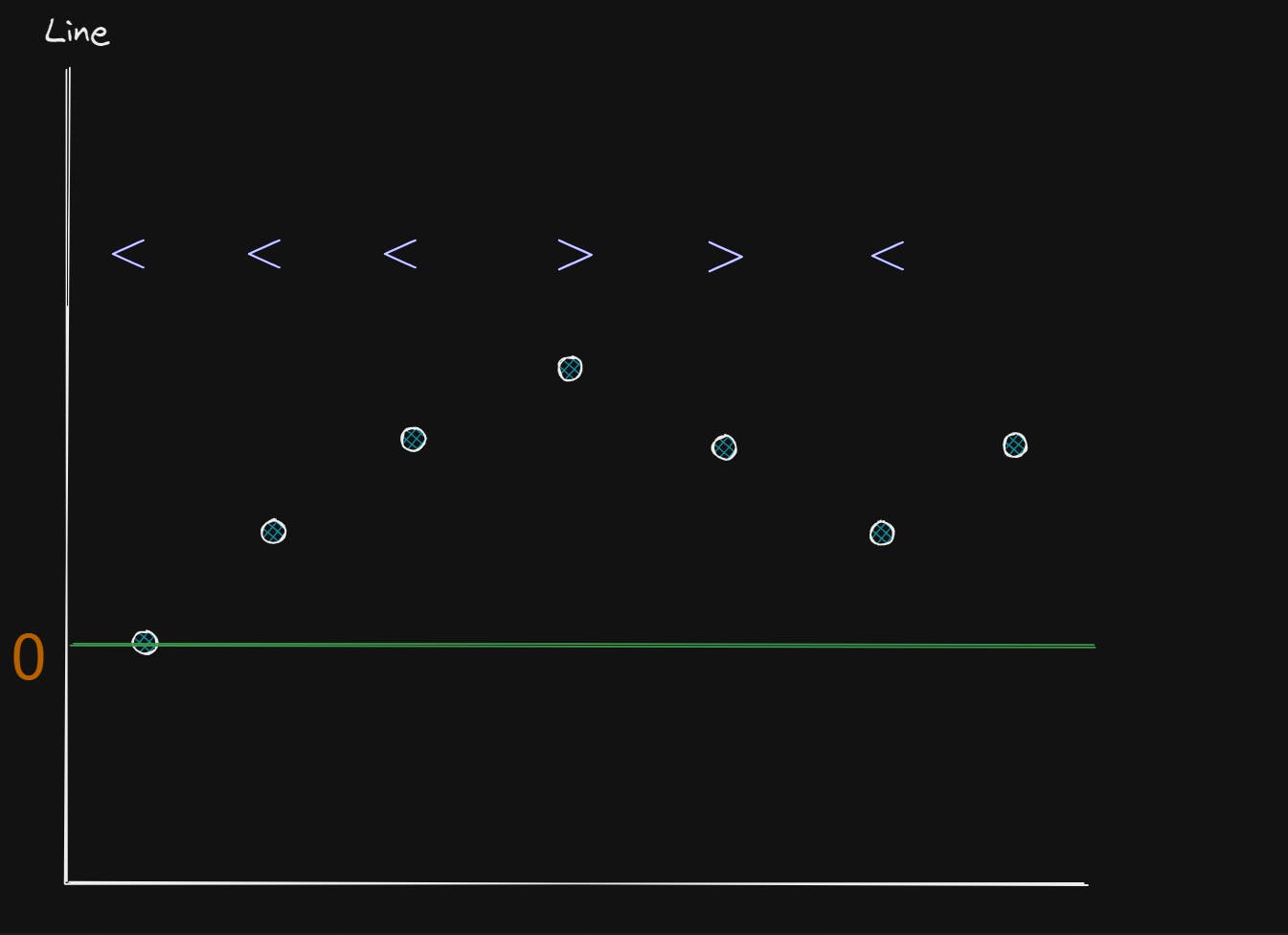
Note :

the points should be allowed to go below 0 too

the stack should be allowed to grow below 0 too

Code Implementing this Algorithm

void wrong_ans(){
    ll t,n; string s;cin >> t;
    while(t--){
        cin >> n >> s;
        ll c=0,mx=0,mn=0;
        for(char ch : s){
            c += (ch=='>') -1 ? : 1 ; // cool trick, huh ?
            mx = max(c,mx) ;
            mn = min(c,mn) ;
        }
        cout << mx + abs(mn) + 1 << "\n" ;
    }  
}

The Edge case that I didn't understand

>><>><>

I thought the compatible array would be something like :-

3 2 1 2 1 0 1 0

or if you start with 2 :-

2 1 0 1 0 -1 0 -1

At this point I also had the simple but really useful epiphany of writing this as :-

3 > 2 > 1 < 2 > 1 > 0 < 1 > 0
2 > 1 > 0 < 1 > 0 > -1 < 0 > -1

So I thought we needed 4 distinct numbers as did my algorithm also predict but the correct answer was 3 - this meant a very huge problem :-

MY ALGORITHM ITSELF WAS LOGICALLY WRONG :(

Correct Solution to the Edge Case

I focused on just this one test case for a long time and it finally clicked :-

3 > 2 > 1 < /*3*/ > 2 > 1 < 2 > 1
2 > 1 > 0 < /*2*/ > 1 > 0 < 1 > 0

The commented number is where I went wrong.

Fundamental problem with my algorithm - What I got Logically Wrong

This idea that NEXT ELEMENT OF ARRAY is always 1 off from current element was the fundamental flawed.

Let me Explain :-

For the test case

> > < > > < >
 3 > 2 > 1 < /*2*/ > 1 > 0 < 1 > 0  // <--- what I thought

Notice that after 1, I PICKED 2 ;
BUT I COULD HAVE PICKED 3 !!

Correct Algorithm - it's just Greedy Lol !

The correct way to think about this approach is very different from what I initially came up with :-

Thought Process :-

Suppose there is a segment of length k that consists of equal characters in s. This segment implies that there are at least k + 1 distinct values in the answer.

So, the answer is at least m + 1, where m is the length of the longest segment of the string that consists of equal characters.

Can we construct the array a which will contain exactly m + 1 distinct values?

It turns out we can do it with the following greedy algorithm :-

Use integers from 0 to m for our compatible array.
Construct it from left to right;
every time we place an element,
- we choose either the largest possible integer we can use (if the next character is >)
  
  OR
- the smallest possible integer we can use ( if the next character is <).

So, the problem basically reduces to finding the longest contiguous subsegment of equal characters in s.

Code Implementation


void solve(){
    ll t,n; string s;cin >> t;
    while(t--){
        cin >> n >> s;
        ll cnt_r=0,mx_r=0,cnt_l=0,mx_l=0;
        for(char c : s){
            if(c=='<'){cnt_r++; mx_r = max(mx_r,cnt_r);}
            else cnt_r = 0;
            if(c=='>'){cnt_l++; mx_l = max(mx_l,cnt_l);}
            else cnt_l = 0;
        }
        cout << max(mx_l,mx_r) + 1 << "\n" ;
    }
}

Learnt a new trick !

This is how I implemented the logic, which I thought was pretty clean and tiddy.

2 Important lessons

Easy way to think about the array I could construct
- The epiphany to write it neatly like :-
  - ```
      3 > 2 > 1 < 2 > 1 > 0 < 1 > 0
```
- Before I had to struggle a bit :-
  - ```
      > > < > > < > 
      3 2 1 2 1 0 1 0
```
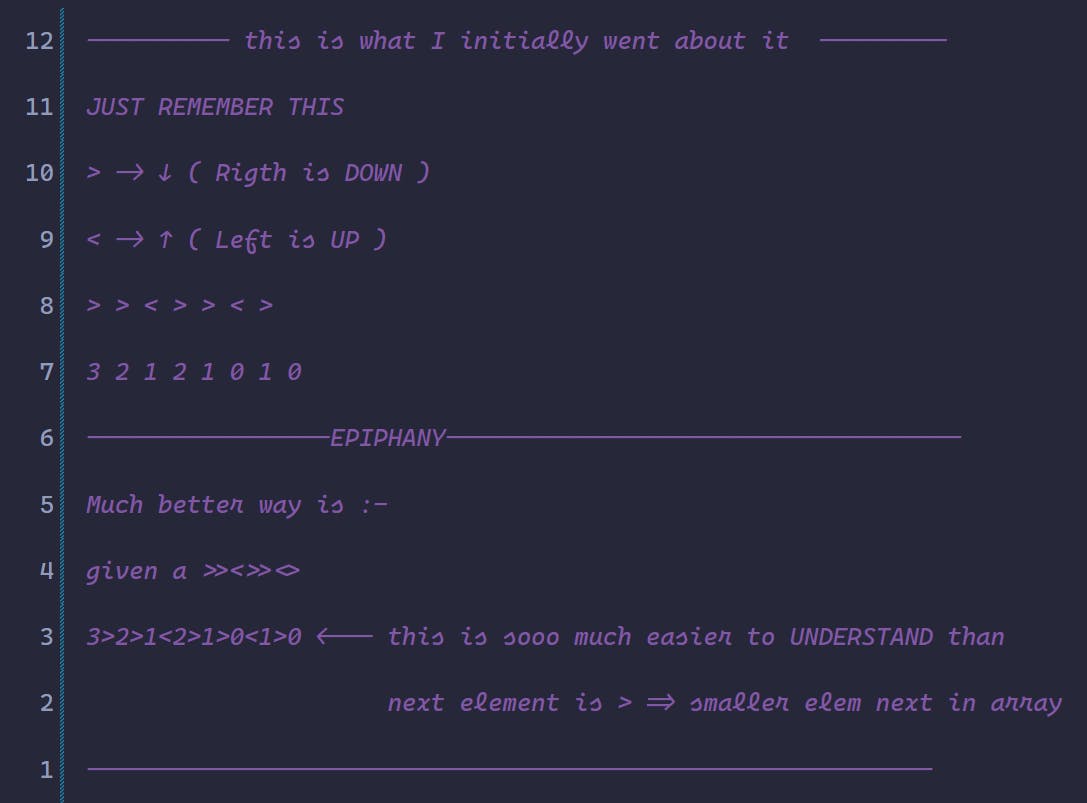
- These are small but really important approaches that gives me much better way to model the stuff I see.

How to find the longest contiguous substring of same character

when it's just 1s and 0s or as given here >s and <s

what happens if it can be anything ? Hashmap ? Nah

  // cnt stores the LENGTH of the longest contiguous substring
  int cnt = 1, now = 1; 

  for(int i = 1; i < n; i++)
  {
      if(s[i] != s[i - 1]) now = 1; // new elem is diff from last elem
      else now++;
      cnt = max(cnt, now);
  }
  cout << cnt + 1 << endl;

Often times when you are given an array, Comparison string gives a the only necessary information we need about the array.

No conclusion section today, this problem just hurt my ego - I need to have a better mindset with these things, sigh.

Thank you,

__CPP_Try_Hard__ ;